Day 2 - Factoring Polynomials

polynomials
factoring
college algebra
Author

Study with Bill

Published

November 12, 2024

Factoring Polynomials

Factoring polynomials is a fundamental concept in algebra that involves rewriting a polynomial as a product of its simpler factors. This process is essential for solving equations, simplifying expressions, and analysing mathematical models.

What Is Factoring?

Factoring means expressing a polynomial as a product of two or more polynomials of lower degree. For example:

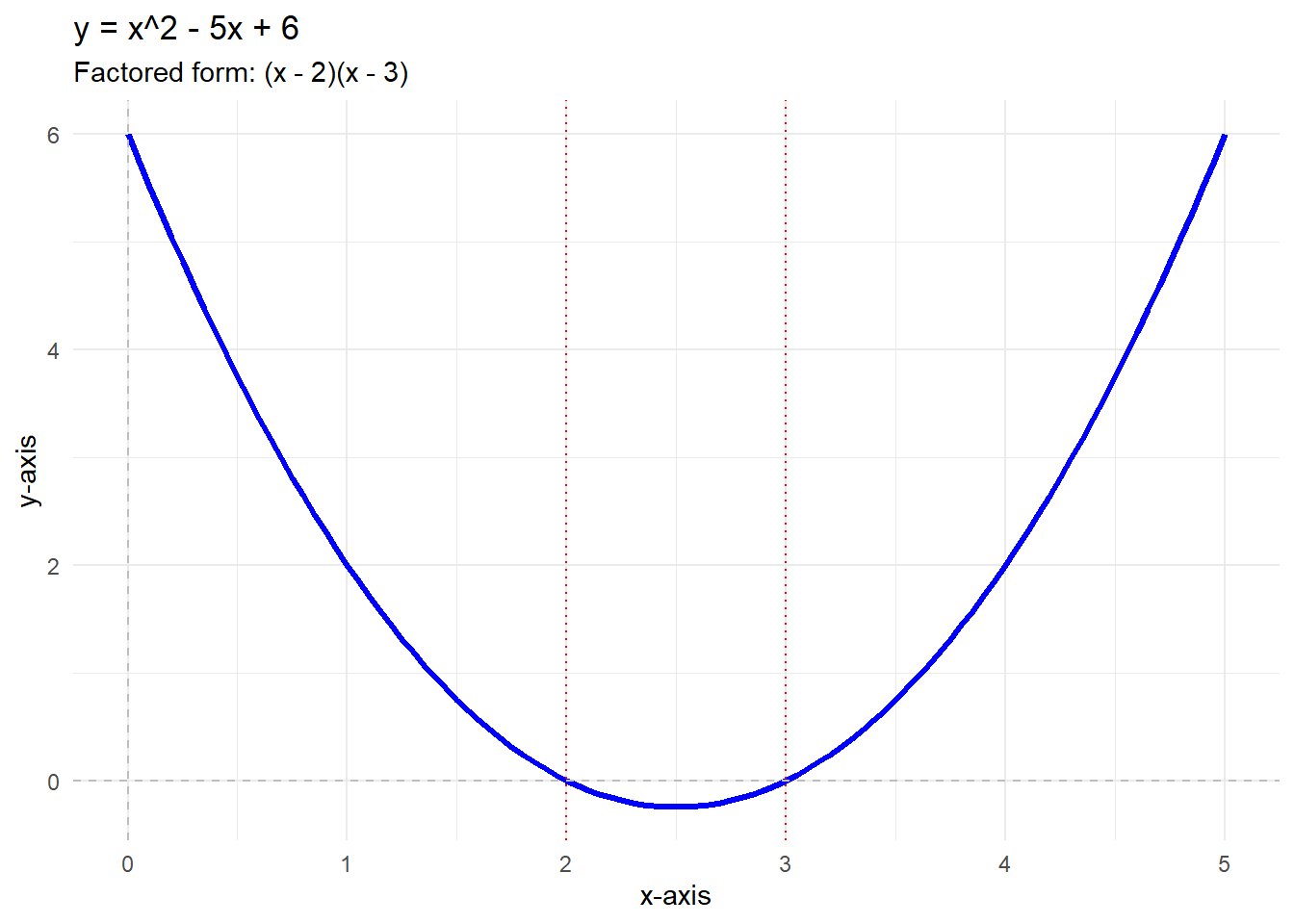
\[x^2 - 5x + 6 = (x - 2)(x - 3)\]

Here, \(x - 2\) and \(x - 3\) are the factors of \(x^2 - 5x + 6\).

The FOIL Method

The FOIL method is a key tool for understanding factoring. FOIL stands for First, Outer, Inner, Last, which represents how you distribute terms when multiplying two binomials.

Example:

Expand \((x + 2)(x + 3)\) using FOIL:

  • First: Multiply the first terms: \(x \cdot x = x^2\)
  • Outer: Multiply the outer terms: \(x \cdot 3 = 3x\)
  • Inner: Multiply the inner terms: \(2 \cdot x = 2x\)
  • Last: Multiply the last terms: \(2 \cdot 3 = 6\)

Combine terms:

\[x^2 + 3x + 2x + 6 = x^2 + 5x + 6\]

Factoring reverses this process.

Common Factoring Techniques

1. Factoring Out the Greatest Common Factor (GCF)

The greatest common factor is the largest term that divides each term of the polynomial.

Example:

\[6x^3 + 9x^2 = 3x^2(2x + 3)\]

2. Factoring by Grouping

For polynomials with four or more terms, group terms to factor them individually, then extract the common factor.

Example:

\[x^3 + 3x^2 + 2x + 6\]

Group terms:

\[(x^3 + 3x^2) + (2x + 6)\]

Factor each group:

\[x^2(x + 3) + 2(x + 3)\]

Extract the common factor:

\[(x^2 + 2)(x + 3)\]

3. Factoring Quadratic Polynomials

Quadratics are polynomials of degree 2, expressed in the form \(ax^2 + bx + c\).

Trial and Error with FOIL:

Find two numbers that multiply to \(ac\) and add to \(b\).

Example:

\[x^2 + 5x + 6\]

Factors of 6 that add to 5 are 2 and 3:

\[x^2 + 5x + 6 = (x + 2)(x + 3)\]

Verify using FOIL:

\[(x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x^2 + 5x + 6\]

4. Factoring Perfect Square Trinomials

A perfect square trinomial is of the form:

\[a^2 + 2ab + b^2 = (a + b)^2\]

Example:

\[x^2 + 6x + 9 = (x + 3)^2\]

Verify using FOIL:

\[(x + 3)(x + 3) = x^2 + 3x + 3x + 9 = x^2 + 6x + 9\]

5. Factoring the Difference of Squares

The difference of squares takes the form:

\[a^2 - b^2 = (a + b)(a - b)\]

Example:

\[x^2 - 16 = (x + 4)(x - 4)\]

Verify using FOIL:

\[(x + 4)(x - 4) = x^2 - 4x + 4x - 16 = x^2 - 16\]

6. Factoring Cubic Polynomials

Sum or Difference of Cubes:

\[a^3 + b^3 = (a + b)(a^2 - ab + b^2)\]
\[a^3 - b^3 = (a - b)(a^2 + ab + b^2)\]

Example:

\[x^3 - 27 = (x - 3)(x^2 + 3x + 9)\]

Solving Polynomial Equations by Factoring

To solve a polynomial equation, factor it and set each factor equal to zero.

Example: Solve \(x^2 - 5x + 6 = 0\).

\[x^2 - 5x + 6 = (x - 2)(x - 3)\]

Set each factor to zero:

\[x - 2 = 0 \quad \text{or} \quad x - 3 = 0\]

Solution: \(x = 2, \, x = 3\).

Practice Problems

  1. Factor \(2x^3 + 4x^2 - 6x\)
  2. Solve \(x^2 + 8x + 16 = 0\)
  3. Factor \(x^4 - 81\)
  4. Factor \(3x^2 - 27\)
  5. Solve \(x^3 + 27 = 0\)

Factoring polynomials, combined with tools like the FOIL method, helps simplify complex problems, verify solutions, and deepen your understanding of algebraic structures. Practice these techniques to master this essential skill!

Thank you for visiting! Explore the other pages for more insights and resources.